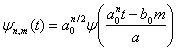¿Qué Onda?: Fundamentos Matemáticos de las WAVELETS. Parte I

Lo que se presenta a continuación es basado en un artículo de Albert Cohen y Jelena Kovacevic llamado Wavelets: The Mathematical Background.

 

Cuando se tiene una señal, existen una gran cantidad de maneras de representarla y en base a lo que necesitamos hacer con dicha señal es que elegimos la manera en que va a ser tratada. El objetivo es que la información obtenida de la señal tenga significado para nosotros, es ahí dónde se pueden lograr varios acercamientos. Entre ellos se encuentran la multiresolución y las transformaciones de dominio.

La multiresolución a grandes rasgos es ir representando la información de manera que los detalles son agregados de forma sucesiva. Para la representación de una señal, uno de los temas que se utilizan ampliamente son las transformaciones de dominio y con ello es menester hablar una de las técnicas más aplicadas, la transformada de Fourier. Con la transformada de Fourier cambiamos la representación de una señal en el dominio del tiempo al dominio de la frecuencia, pero no podemos saber en que instante de tiempo está ubicada la frecuencia, esto es en algunos casos una limitación.

Una manera de darnos una idea de la localización en tiempo de la frecuencia es construir bloques y aplicarles la transformada de Fourier. Si tenemos que es una señal de frecuencia, con Fourier obtenemos un pico en la frecuencia dada. A partir de esto podemos expresar dónde es la ventana usada para localizar la frecuencia en el tiempo, a esto se le llama Short-time Fourier Transform (STFT). Una de las principales desventajas con la STFT es que la localización en el espacio tiempo es fija. Con las wavelets se tiene un acercamiento diferente, la localización de la frecuencia es logarítmica y proporcional al nivel de frecuencia.

Se puede definir una familia de funciones de la siguiente manera que nos permita tener una representación en la escala del tiempo

,

(1)

dónde es una función fija llamada “wavelet madre”, a representa el escalamiento de la función y b son los corrimientos en el tiempo.

Basado en la función representada en (1) y tomando en cuenta que es un espacio de Hilbert, se define la transformada de una función f de la siguiente manera:

(2)

Para que la transformada (2) pueda ser invertible, se tiene elegir una de manera que cumpla con la condición de admisibilidad mostrada a continuación:

(3)

Y para asegurar que la integral es finita se debe cumplir que . En base a lo anterior tenemos que se puede reconstruir mediante:

(4)

Prácticamente, una transformada wavelet continua se aplica a una serie de puntos discretos de manera . Si se restringe la transformada continua wavelet de manera que , dónde entonces para valores fijos y . Entonces podemos definir la función wavelet de manera general cómo:

,

(5)

Para saber si la transformada wavelet en el caso discreto caracteriza completamente la función f y logra reconstruirla de manera estable, se requiere introducir el concepto de frames.

Para que un frame exista, y por lo tanto reconstrucción a partir de la wavelet, se debe tener una secuencia en un espacio de Hilbert H si para cada x perteneciente al espacio H se cumple lo siguiente:

(6)

En dónde los límites son independientes de x. A dicha secuencia se le asocia al operador F que representa a y también se desprende de ahí F* que asocia la sumatoria de las secuencias en .

La desigualdad expresada en (6) puede ser expresada en términos del operador hermitiano F* F de manera que:

(7)

En base a lo anterior podemos definir una secuencia dada por que también constituye un frame llamado dual frame con límites en y se asocia con el operador llamado por lo consiguiente tenemos que:

(8)

Y también tenemos que así que una x que forma parte del espacio de Hilbert es representada por:

(9)

Para reconstruir x debemos conocer . Teniendo en cuenta que:

(10)

Dónde el operador residual satisface lo siguiente:

(11)

Sustituyendo en (7) nos da como resultado la siguiente ecuación:

(12)

Si tenemos que A=B=1 después de renormalizar, entonces podemos definir lo siguiente:

(13)

De manera que elegimos valores de A-B/A+B que se aproximan a cero y también A y B de manera arbitraria cercanos a uno seguido de una renormalización, eligiendo valores a₀ y b₀ cercanos a uno y cero respectivamente. Lo anterior significa que se ha hecho un sobre-muestreo de la wavelet continua en un arreglo bastante denso. Una de las aplicaciones más usadas para usar el sobre-muestreo empleando frames es el de reducir el error de reconstrucción con una relación basada en el sobre-muestreo.

 

Continuará…